Background
In 1848, Max Bezzel first posed the Eight Queens Problem: Place eight queens on a chessboard so that no two queens attack each other. This problem was generalized in 1869 to the N-Queens problem (N mutually non-attacking queens on an N-by-N chessboard).
In 1995, Michael Anshel of the City University of New York presented the following problem to an Artificial Intelligence seminar: if we remove some of the squares of the chessboard, can we place more than N queens on the "partial chessboard" that remains? In 1998, Anshel's student, Kaiyan Zhao, defended her doctoral thesis entitled "The Combinatorics of Chessboards," which considered "The Queens Problem on a Partial Chessboard". Among other things, Zhao proved that three pawns are necessary and sufficient to allow six nonattacking queens on a five-by-five board.
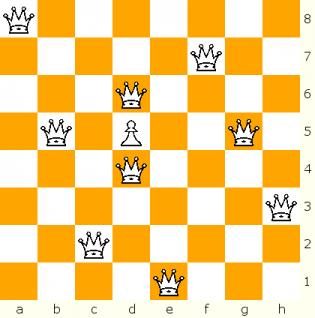
In 2004, the Chess Variant Pages sponsored a contest that posed the following question (credited to Wim Henk Boedlander): We can put nine mutually non-attacking queens on an eight-by-eight board if we put some pawns on the board to block queen attacks. How few pawns are necessary? The answer turns out to be 1, as you can see in the picture below. The Nine Queens Problem contest can be found at http://www.chessvariants.org/problems.dir/9queens.html.
In 1995, Michael Anshel of the City University of New York presented the following problem to an Artificial Intelligence seminar: if we remove some of the squares of the chessboard, can we place more than N queens on the "partial chessboard" that remains? In 1998, Anshel's student, Kaiyan Zhao, defended her doctoral thesis entitled "The Combinatorics of Chessboards," which considered "The Queens Problem on a Partial Chessboard". Among other things, Zhao proved that three pawns are necessary and sufficient to allow six nonattacking queens on a five-by-five board.
In 2004, the Chess Variant Pages sponsored a contest that posed the following question (credited to Wim Henk Boedlander): We can put nine mutually non-attacking queens on an eight-by-eight board if we put some pawns on the board to block queen attacks. How few pawns are necessary? The answer turns out to be 1, as you can see in the picture below. The Nine Queens Problem contest can be found at http://www.chessvariants.org/problems.dir/9queens.html.
The contest participants soon asked about generalizations, such as "How many pawns would it take on a larger board?" It turns out that for N > 5, we need to put only one pawn on the board in order to allow us to place N+1 nonattacking queens on the board. More generally, for each k > 0, if N is large enough we can place N + k queens and k pawns on an N-by-N board so that none of the queens attack each other. For more details, see the Papers page.
Here is a partial list of unsolved problems related to the N+k Queens Problem:
Here is a partial list of unsolved problems related to the N+k Queens Problem:
- For a particular N and k, how many ways are there to place N + k queens and k pawns on an N-by-N board so that no two queens attack each other? We've done some computer searches and come up with some numbers.
- Where can the pawns go?
- What happens if we look at non-square (e.g. rectangular, toroidal, hexagonal. three-dimensional) boards?
- On a standard chessboard, if you want to place queens on the board so that every square is attacked or occupied, the minimum number of queens you need is five. If we wanted to increase or decrease that number, how many pawns would we need to place on the board, and where? (And how many pawns would we need on other-sized boards to increase or decrease the number of queens needed to dominate those boards?)
- What happens to other graph-theoretic parameters when we place pawns on a chessboard?
- What happens if we use pieces other than queens, such as bishops or rooks or even nonstandard pieces like the amazon (combination of queen and knight)?