Welcome!
Welcome! This site is a collection of materials related to the N + k Queens Problem:
Given a positive integer N and a nonnegative integer k, can we place k pawns and N + k queens on an chessboard with N rows and N columns so that every pair of queens on the same row, column, or diagonal have at least one pawn between them?
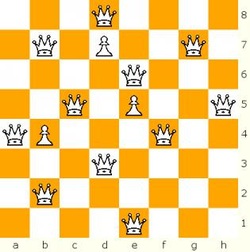A solution to the 8 + 3 Queens Problem
Here's an example of a solution to the 8 + 3 Queens Problem. On an 8-by-8 board, there are 3 pawns and 8+3 = 11 queens,. Each pair of queens on the same row, column, or diagonal have at least one pawn between them; i.e., none of the queens "attack" any of the other queens.
For more information on the origins of this problem, see the Background page.
To see some of what we've found out about this problem and related problems, see the Papers page and the Talks page.
If you'd like to see more solutions or find out how many solutions there are for some values of N and k, see the Solutions page.
The Programs page has programs related to searching for solutions.
To see what others are saying about the N + k Queens Problem, check out the Other Links page.
If you have comments or questions, feel free to email [email protected].
For more information on the origins of this problem, see the Background page.
To see some of what we've found out about this problem and related problems, see the Papers page and the Talks page.
If you'd like to see more solutions or find out how many solutions there are for some values of N and k, see the Solutions page.
The Programs page has programs related to searching for solutions.
To see what others are saying about the N + k Queens Problem, check out the Other Links page.
If you have comments or questions, feel free to email [email protected].
Acknowledgments
This website is maintained by Doug Chatham. Thanks to the colleagues who have collaborated in this research, including Robin Blankenship, Paul Burchett, Maureen Doyle, Gerd Fricke, Walter Kosters, Duane Skaggs, and Jeff Ward. Thanks also to the students who have assisted us, including Bethany Alloway, Jonathon Byrd, Kelly Gripshover, Craig Hamilton, Joe Harless, Logan Higginbotham, William Holbrook, Casey Hufford, Robert Jeffers, Iris Johnson, Michael McGinnis, John Miller, Blake Nickell, Jon Reitmann, Amber Rogers, Brian Salyer, Biswas Sharma, Luke Thompson, Nick Wahle, and Matt Wolff.
The research described in this website was partially supported by NSF KY-EPSCoR Research Enhancement Grant UKRF 3046884400-07-419, NASA KY-EPSCoR grant NCC5-571, Morehead State University Faculty Research Grant 225229, and many MSU Undergraduate Research Fellowships.
Some of the chess diagrams on this site were generated by CVP Game Courier.
The research described in this website was partially supported by NSF KY-EPSCoR Research Enhancement Grant UKRF 3046884400-07-419, NASA KY-EPSCoR grant NCC5-571, Morehead State University Faculty Research Grant 225229, and many MSU Undergraduate Research Fellowships.
Some of the chess diagrams on this site were generated by CVP Game Courier.